Најкраћи путеви од једног чвора
Тежински графови
У наставку ћемо претпоставити да радимо са тежинским графовима тј. да је свакој грани графа придружена нека тежина (то обично може бити дужина гране тј. растојање између два суседна чвора).
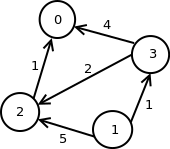
Тежински граф ћемо обично представљати или матрицом повезаности у којој се уместо логичких вредности чувају тежине грана (уз неку специјалну нумеричку вредност која означава да чворови нису повезани) или листама повезаности где се у сваком елементу листе повезаности чува индекс крајњег чвора и тежина гране.
У језику C++ репрезентација графа може бити било матрица облика
Tezina A[MAX][MAX];било динамички алоцирана матрица облика
vector<vector<Tezina>> A(n);
for (int i = 0; i < n; i++)
A[i].resize(n);Ако користимо листе повезаности, онда можемо употребити структуру података облика
vector<vector<pair<Cvor, Tezina>> A(n);која нам омогућава да веома једноставно додајемо нове гране.
A[cvorOd].emplace_back(cvorDo, tezina);При том тип Tezina означава тежине грана (оне могу бити
цели или реални бројеви), док тип Cvor означава индексе
чворова (и они су по правилу целобројни).
Дајкстрин алгоритам
Дајкстрин алгоритам је алгоритам који нам омогућава да ефикасно пронађемо најкраће путеве од једног фиксираног чвора, до свих осталих чворова у графу. Посебно, њиме можемо наћи најкраће растојање између два унапред дата чвора. У наставку ћемо претпоставити да су дужине свих грана у графу ненегативне.
Ако најкраћи пут од чвора \(u\) до било ког чвора \(v\) пролази преко неког чвора \(w\), тада је за одређивање тог најкраћег пута потребно претходно познавати најкраћи пут од \(u\) до \(w\). Због тога је основна идеја алгоритма да се најкраћи путеви од чвора \(u\) до осталих чворова одређују у растућем редоследу у односу на дужину најкраћег пута од \(u\). Прво се одређује најкраћи пут од \(u\) до \(u\) (који је једнак нули), затим се проналази чвор који је најближи чвору \(u\) и најкраће растојање до њега итд.
Инваријанта овог алгоритма је то да након \(k\) корака извршавања алгоритма умемо да пронађемо \(k\) чворова nајближих почетном чвору \(v\) и дужине најкраћих путева до њих. У почетку знамо само да је чвор \(v\) најближи сам себи и да је дужина пута од \(v\) до \(v\) једна нули. Означимо са \(V_k\) скуп који се састоји од \(k\) најближих чворова чвору \(v\), укључујући и \(v\). Проблем је пронаћи чвор \(w\) који је најближи чвору \(v\) међу чворовима ван \(V_k\), и пронаћи дужину најкраћег пута од \(v\) до \(w\). Најкраћи пут од \(v\) до \(w\) може да садржи само чворове из \(V_k\). Он не може да садржи неки чвор \(y\) ван \(V_k\), јер би чвор \(y\) био ближи чвору \(v\) од \(w\). Према томе, да бисмо пронашли чвор \(w\), довољно је да проверимо гране које спајају чворове из \(V_k\) са чворовима који нису у \(V_k\); све друге гране се за сада могу игнорисати. Нека је \((u, z)\) грана таква да је \(u \in V_k\) и \(z \notin V_k\). Таква грана одређује пут од \(v\) до \(z\) који се састоји од најкраћег пута од \(v\) до \(u\) (који је већ познат) и гране \((u, z)\). Довољно је упоредити све такве путеве и изабрати најкраћи међу њима. Дакле, чвор \(w\) је чвор за који је најмања дужина
\[\min\{d(v, u) + d(u, w)\ |\ u\in V_k\}.\]
При том, \(d(v, u)\) нам је већ познато минимално растојање од \(v\) до \(u\), док је \(d(u, w)\) дужина гране између \(u\) и \(w\).
У имплементацији можемо у једном низу одржавати текуће процене најкраћих растојања од \(v\) до сваког другог чвора. У почетку у низ на место чвора \(v\) уписујемо 0, док је дужина свих других путева непозната и у низ уписујемо \(+\infty\). Чворови који се налазе у тренутном скупу \(V_k\) ћемо на неки начин означавати (на пример, одржавањем помоћног низа у коме логичким вредностима обележавамо означене чворове). У сваком кораку из низа бирамо онај неозначени чвор \(w\) који има тренутно најмање растојање и придодајемо га у скуп \(V_k\) тако што га означавамо. Његово тренутно растојање од чвора \(v\) (које је уписано у низу на месту чвора \(w\)) је уједно и најкраће растојање од чвора \(v\) до свих чворова ван \(V_k\). Зато је \(w\) чвор који је \(k+1\) и њиме проширујемо скуп \(V_k\). У том тренутку ажурирамо остала растојања у низу. Нагласимо да приликом проширивања скупа \(V_k\) чвором \(w\) нема потребе ажурирати путање из чворова који се већ налазе у \(V_k\), већ је довољно ажурирати само путање које воде преко \(w\). То радимо тако што за суседе чвора \(w\) проверавамо да ли је збир најкраћег пута од \(v\) до \(w\) (тренутна вредност у низу на месту чвора \(w\)) и дужине гране од \(w\) до тог чвора мања од тренутне процене најмање дужине пута дог тог чвора (тј. тренутне вредности у низу на месту тог чвора).
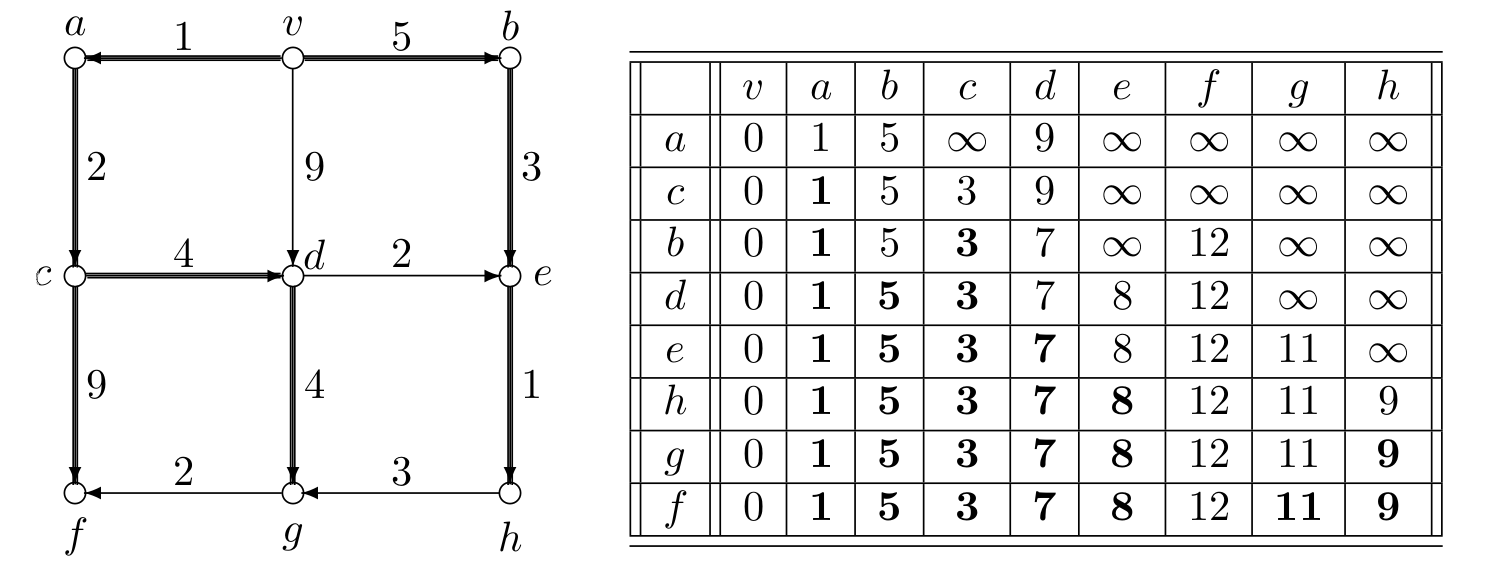
Пример. Пример извршавања Дајкстриног алгоритма за налажење најкраћих путева од чвора \(v\) у графу дат је на слици. Прва врста односи се само на путеве од једне гране из \(v\). Бира се најкраћи пут, у овом случају он води ка чвору \(a\). Друга врста показује поправке дужина путева укључујући сада све путеве од једне гране из \(v\) или \(a\), и најкраћи пут сада води до \(c\). У свакој линији бира се нови чвор, и приказују се дужине тренутних најкраћих путева од \(v\) до свих чворова. Подебљана су растојања за која се поуздано зна да су најкраћа (ти чворови су означени).
Пошто је у сваком кораку потребно проналазити минимум скупа бројева и након тога уклањати минимум из скупа, уместо низа, можемо користити ред са приоритетом у којем чувамо скуп неозначених чворова, уређен на основу тренутне процене растојања од чвора \(v\). За то можемо користити ред са приоритетом (тј. хип). Кључни проблем ове имплементације је то што се након проширивања скупа \(V_k\) неке процене дужине пута смањују, па је потребно ажурирати вредности у реду са приоритетом. Редови са приоритетом обично не подржавају директно такве операције. Један начин је да се креира специјализована имплементација која би подржала могућност смањивања вредности у реду, а друга је да се употреби тзв. техника лењог брисања. У том случају се након смањивања процене растојања неког чвора у ред просто додаје нови елемент који представља смањено растојање. Тиме се за исти чвор у реду истовремено чува више разних процена растојања. У тренутку када се чвор \(w\) убацује у \(V_k\) из реда ће бити извађено његово најмање растојање од \(v\) (ако за чвор \(w\) постоје неке раније процене, оне ће сигурно бити веће и још ће се налазити у реду). Ако се касније деси да се из реда извади чвор \(w\) на основу неке раније процене, то ћемо лако препознати на основу тога што је \(w\) већ раније био убачен у чвор \(V_k\) и означен, тако да ћемо тај елемент извађен из реда просто занемарити и прећи ћемо на наредни елемент из реда.
Најкраћи путеви од једног чвора
Тежински графови
У наставку ћемо претпоставити да радимо са тежинским графовима тј. да је свакој грани графа придружена нека тежина (то обично може бити дужина гране тј. растојање између два суседна чвора).

Тежински граф ћемо обично представљати или матрицом повезаности у којој се уместо логичких вредности чувају тежине грана (уз неку специјалну нумеричку вредност која означава да чворови нису повезани) или листама повезаности где се у сваком елементу листе повезаности чува индекс крајњег чвора и тежина гране.
У језику C++ репрезентација графа може бити матрица облика
Tezina[,] A = new Tezina[MAX, MAX];Ако користимо листе повезаности, онда можемо употребити структуру података облика
var A = new List<Tuple<Cvor, Tezina>>[n];
for (int i = 0; i < n; i++)
A[i] = new List<Tuple<Cvor, Tezina>>();која нам омогућава да веома једноставно додајемо нове гране.
A[cvorOd].Add(Tuple.Create(cvorDo, tezina));При том тип Tezina означава тежине грана (оне могу бити
цели или реални бројеви), док тип Cvor означава индексе
чворова (и они су по правилу целобројни).
Дајкстрин алгоритам
Дајкстрин алгоритам је алгоритам који нам омогућава да ефикасно пронађемо најкраће путеве од једног фиксираног чвора, до свих осталих чворова у графу. Посебно, њиме можемо наћи најкраће растојање између два унапред дата чвора. У наставку ћемо претпоставити да су дужине свих грана у графу ненегативне.
Ако најкраћи пут од чвора \(u\) до било ког чвора \(v\) пролази преко неког чвора \(w\), тада је за одређивање тог најкраћег пута потребно претходно познавати најкраћи пут од \(u\) до \(w\). Због тога је основна идеја алгоритма да се најкраћи путеви од чвора \(u\) до осталих чворова одређују у растућем редоследу у односу на дужину најкраћег пута од \(u\). Прво се одређује најкраћи пут од \(u\) до \(u\) (који је једнак нули), затим се проналази чвор који је најближи чвору \(u\) и најкраће растојање до њега итд.
Инваријанта овог алгоритма је то да након \(k\) корака извршавања алгоритма умемо да пронађемо \(k\) чворова nајближих почетном чвору \(v\) и дужине најкраћих путева до њих. У почетку знамо само да је чвор \(v\) најближи сам себи и да је дужина пута од \(v\) до \(v\) једна нули. Означимо са \(V_k\) скуп који се састоји од \(k\) најближих чворова чвору \(v\), укључујући и \(v\). Проблем је пронаћи чвор \(w\) који је најближи чвору \(v\) међу чворовима ван \(V_k\), и пронаћи дужину најкраћег пута од \(v\) до \(w\). Најкраћи пут од \(v\) до \(w\) може да садржи само чворове из \(V_k\). Он не може да садржи неки чвор \(y\) ван \(V_k\), јер би чвор \(y\) био ближи чвору \(v\) од \(w\). Према томе, да бисмо пронашли чвор \(w\), довољно је да проверимо гране које спајају чворове из \(V_k\) са чворовима који нису у \(V_k\); све друге гране се за сада могу игнорисати. Нека је \((u, z)\) грана таква да је \(u \in V_k\) и \(z \notin V_k\). Таква грана одређује пут од \(v\) до \(z\) који се састоји од најкраћег пута од \(v\) до \(u\) (који је већ познат) и гране \((u, z)\). Довољно је упоредити све такве путеве и изабрати најкраћи међу њима. Дакле, чвор \(w\) је чвор за који је најмања дужина
\[\min\{d(v, u) + d(u, w)\ |\ u\in V_k\}.\]
При том, \(d(v, u)\) нам је већ познато минимално растојање од \(v\) до \(u\), док је \(d(u, w)\) дужина гране између \(u\) и \(w\).
У имплементацији можемо у једном низу одржавати текуће процене најкраћих растојања од \(v\) до сваког другог чвора. У почетку у низ на место чвора \(v\) уписујемо 0, док је дужина свих других путева непозната и у низ уписујемо \(+\infty\). Чворови који се налазе у тренутном скупу \(V_k\) ћемо на неки начин означавати (на пример, одржавањем помоћног низа у коме логичким вредностима обележавамо означене чворове). У сваком кораку из низа бирамо онај неозначени чвор \(w\) који има тренутно најмање растојање и придодајемо га у скуп \(V_k\) тако што га означавамо. Његово тренутно растојање од чвора \(v\) (које је уписано у низу на месту чвора \(w\)) је уједно и најкраће растојање од чвора \(v\) до свих чворова ван \(V_k\). Зато је \(w\) чвор који је \(k+1\) и њиме проширујемо скуп \(V_k\). У том тренутку ажурирамо остала растојања у низу. Нагласимо да приликом проширивања скупа \(V_k\) чвором \(w\) нема потребе ажурирати путање из чворова који се већ налазе у \(V_k\), већ је довољно ажурирати само путање које воде преко \(w\). То радимо тако што за суседе чвора \(w\) проверавамо да ли је збир најкраћег пута од \(v\) до \(w\) (тренутна вредност у низу на месту чвора \(w\)) и дужине гране од \(w\) до тог чвора мања од тренутне процене најмање дужине пута дог тог чвора (тј. тренутне вредности у низу на месту тог чвора).
Пример. Пример извршавања Дајкстриног алгоритма за налажење најкраћих путева од чвора \(v\) у графу дат је на слици. Прва врста односи се само на путеве од једне гране из \(v\). Бира се најкраћи пут, у овом случају он води ка чвору \(a\). Друга врста показује поправке дужина путева укључујући сада све путеве од једне гране из \(v\) или \(a\), и најкраћи пут сада води до \(c\). У свакој линији бира се нови чвор, и приказују се дужине тренутних најкраћих путева од \(v\) до свих чворова. Подебљана су растојања за која се поуздано зна да су најкраћа (ти чворови су означени).

Пошто је у сваком кораку потребно проналазити минимум скупа бројева и након тога уклањати минимум из скупа, уместо низа, можемо користити ред са приоритетом у којем чувамо скуп неозначених чворова, уређен на основу тренутне процене растојања од чвора \(v\). За то можемо користити ред са приоритетом (тј. хип). Кључни проблем ове имплементације је то што се након проширивања скупа \(V_k\) неке процене дужине пута смањују, па је потребно ажурирати вредности у реду са приоритетом. Редови са приоритетом обично не подржавају директно такве операције. Један начин је да се креира специјализована имплементација која би подржала могућност смањивања вредности у реду, а друга је да се употреби тзв. техника лењог брисања. У том случају се након смањивања процене растојања неког чвора у ред просто додаје нови елемент који представља смањено растојање. Тиме се за исти чвор у реду истовремено чува више разних процена растојања. У тренутку када се чвор \(w\) убацује у \(V_k\) из реда ће бити извађено његово најмање растојање од \(v\) (ако за чвор \(w\) постоје неке раније процене, оне ће сигурно бити веће и још ће се налазити у реду). Ако се касније деси да се из реда извади чвор \(w\) на основу неке раније процене, то ћемо лако препознати на основу тога што је \(w\) већ раније био убачен у чвор \(V_k\) и означен, тако да ћемо тај елемент извађен из реда просто занемарити и прећи ћемо на наредни елемент из реда.
